I solved this problem on POI a while back, and I felt the ideas used in this problem are quite versatile. I was so intrigued by this problem that I decided to write a short summary of my intuitions and motivations in the solving process. A little bit of knowledge on linear transformations and matrices will be necassary.

If you want to try out your idea, here’s the problem link. If statement is too big for you, here’s an abridged problem statement:

---

You are given given $n$ points where the $i$ th point is $(x_i, y_i)$. You are also given four integers $X_1, Y_1, X_2, Y_2$. For each point $(x_i, y_i)$ consider the angle formed by rays $(x_i, y_i)$ to $(x_i + X_1, y_i + Y_1)$ and $(x_i, y_i)$ to $(x_i + X_2, y_i + Y_2)$. $i$ th point is manually turned-on on $i$ th minute, and if a point is turned on, it illuminates the area between its angle. Additionally, if the $i$ th point is illuminated by at least $k_i$ other points, it automatically turns on and starts illuminating light. Determine for each point the first time they will start producing light.

---

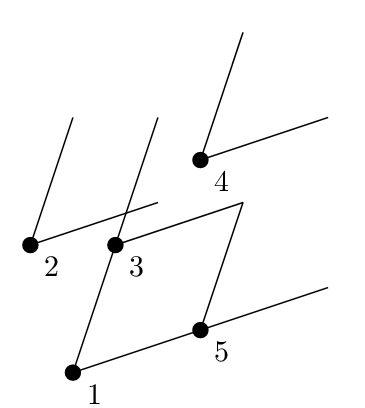
The problem sure does look intimidating. Okay, let’s see what we have in our favor and how to exploit them. First of all, angles formed by each point are equal. We must use this properly. Also constraints give off a data structure-ish vibe, so it may be fruitful to model this problem from a data structure point of view. Okay, let’s try to solve an easier version of this problem. Suppose the angle formed by each point is $90$ degrees, and the rays are parallel to $x$ and $y$ axis (and they directed towards the positive side). If you are still confused, it looks like this. This is the closest variant of this problem that common data structures can handle.

When does a point gets illuminated by another point? In our modified problem, this condition is rather simple. A point $(x_i, y_i)$ gets illuminated by another point $(x_j, y_j)$ if and only if $x_j \leq x_i$ and $y_j \leq y_i$. We want something like this in the original problem. So, let’s investigate why does conditions become simpler in the modified version. One might be tempted to point out the angles are now $90$ degrees, hence the oversimplification. But a closer inspection will tell you this is not the case. The simplicity actually lies on the fact that rays that shoots off the points are axis parallel.

A skeptical reader might be in despair now. Our solution will only work when the rays are axis parallel. There’s not even a subtask devoted this case. This does not look remotely close to what actual solution might be. In order to progress from here, we have to learn NOT to play by the rules. Let’s imagine a coordinate system, but its axes are not perpendicular to each other, instead they form a certain angle!! In particular, they form the same angle each point in our input forms. This kind of transformation is called linear transformation. (If you are interested to learn more about this: click. One example of such transformation is depicted below:

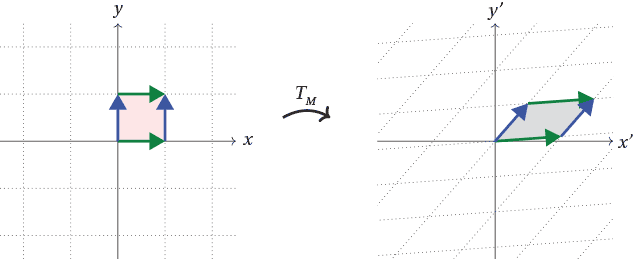
So if the axes of our coordinate system forms the same angle as the points in our problem, we can still apply the previous condition: A point $(x_i, y_i)$ gets illuminated by another point $(x_j, y_j)$ if and only if $x_j \leq x_i$ and $y_j \leq y_i$. Here, $(x_i, y_i)$ and $(x_j, y_j)$ are not coordinates of the the cartesian plane (the one where axes are perpendicular), but rather they are the coordinates of our modified coordinate system. Once we find these modified coordinates for each point, it boils down to the easy variant that we discussed earlier. Here’s how to find the modified coordinate of each point: (Some calculations are involved)

We know every point on cartesian system can be expressed using a linear combination of $\hat{i}$ and $\hat{j}$ where

\[\hat{i} = \begin{bmatrix} 1\\ 0 \end{bmatrix} \, \, \hat{j} = \begin{bmatrix} 0\\ 1 \end{bmatrix}\]

In other words, $\hat{i}$ and $\hat{j}$ are unit vectors parallel to $x$ and $y$ axis respectively.

But we want the axes to be parallel to the rays that are shooted from each point. For this modified coordinate system, we choose

\[\hat{i} = \begin{bmatrix} X_1\\ Y_1 \end{bmatrix} \, \, \hat{j} = \begin{bmatrix} X_2\\ Y_2 \end{bmatrix}\]

Suppose we want to find the modfied coordinate of point $(x, y)$. Let’s assume the modified coordinate is $(a, b)$. So,

\[a\hat{i} + b\hat{j} = \begin{bmatrix} x\\ y \end{bmatrix}\] \[a\begin{bmatrix} X_1\\ Y_1 \end{bmatrix} + b \begin{bmatrix} X_2\\ Y_2 \end{bmatrix} = \begin{bmatrix} x\\ y \end{bmatrix}\] \[\begin{bmatrix} aX_1 + bX_2\\ aY_1 + bY_2 \end{bmatrix} = \begin{bmatrix} x\\ y \end{bmatrix}\]

Solving for $a$ and $b$ yields [(a, b) = \left ( \frac{xY_1 - yX_1}{X_{2}Y_{1} - Y_{2}X_{1}}, \frac{yX_2 - xY_2}{X_{2}Y_{1} - Y_{2}X_{1}} \right )]

This the coordinate we’ll use from for point $(x, y)$.

One problem still persists. Coordinates of our modified system will be floating point numbers, which you and I both hate. Notice that, as a denominator, the term $X_{2}Y_{1} - Y_{2}X_{1}$ is present, which remains constant throughout the problem. So we can multiply each coordinate by in our modified coordinate system by $\mid X_{2}Y_{1} - Y_{2}X_{1} \mid$ (by this, we are essentially scaling the coordinates, so this doesn’t change our answers). This will make everything integer numbers. One more thing, we have to take care of the case where $X_{2}Y_{1} - Y_{2}X_{1} = 0$ (this happens when the angle is zero). This case is relatively straight-forward and is, therefore, ommited here. Armed with these, we can focus on the earlier problem. Solving that will solve the entire thing.

Our problem has reduced to a purely data structure problem. Suppose the point $i$ will start producing light in $t_i$ th time. We can calculate the values of $t_i$ with a blend of dynamic programming and greedy approach. Let assume points $p_1, p_2, p_3, \dots, p_m$ illuminates the $i$ th point. Points $p_1, p_2, p_3, \dots, p_m$ start producing light in times $t_{p_1}, t_{p_2}, t_{p_3}, \dots, t_{p_m}$. Assume that the points are sorted according to the time they start producing light. In other words, $t_{p_1} \leq t_{p_2} \leq t_{p_3} \leq \dots \leq t_{p_m}$. Then value of $t_i$ will be: [t_i = \min{(i, t_{p_{k_i}})}]

This is rather slow. There might be $O(n)$ points that illuminates a particular point. Also in order to find the value of $t_i$, we have to sort the points according to the time. So calculating the value of a single $t_i$ takes $O(n \log n)$ time. So total runtime would be $O(n^{2} \log n)$ But we can improve upon the previous solution. There are two ways. One is to use use a segment tree with a treap in each node to calculate the values of $t$ faster. This yields a $O(n \log^{2}n)$ solution with heavy constant factor. This only gets 70 points. 100 point solution requires a somewhat different approach using Parallel Binary Search. If you do not know it, I urge you to learn it first from that excellent codeforces blog. If you are already familiar with the concept, this becomes a simple exercise. We have to binary search on the values of $t_i$ simultaneously. I’ll only describe the key idea component of the algorithm here:

Suppose we have a function solve(l, r, S) that takes a range $[l, r]$ and a set of points $S$ whose $t_i$ values lies within that range. Set $m = \frac{l + r}{2}$. We want to find out which of the points in set $S$ have $t_i$ values in range $[l, m]$. Assume points of $S$ are sorted according to their $x$ coordinate with ties broken by $y$ coordinate. We process points in this sorted order one by one. Also, let’s create a BBST $^1$ which will store the $y$ coordinates of the points whose value of $t$ lies in range $[l, m]$ (found before processing the current point). Suppose we are now processing the $i$ th point. If i lies in range $[l, m]$ then we are sure that $t_i$ also lies in range $[l, m]$ Otherwise, find out the number of values in the BBST that are less than the $y$ coordinate of the currently processed point. Suppose this number is $h$. If $h \geq k_i$ then we can be sure $t_i$ again lies in range $[l, m]$. If none the previous cases hold, $t_i$ cannot be in range $[l, m]$. If the $i$ th point is lies within range $[l, m]$, then we insert its $y$ coordinate in the BBST and move onto the next point. By performing the above algorithm for all points in $S$, we can identify which of the points lie in range $[l, m]$ (let the set of such points be $T$). This takes us $O(|S| \log n)$ time. Now we can call solve(l, m, T)and solve(m + 1, r, S \ T) to recursively solve the remaining problem. So, the complexity of the parallel binary search is $O(n \log^{2} n)$ time with low constant factor.

$^{1}$ It’s possible to use a binary indexed tree instead of BBST if $y$ coordinates of the points are compressed